构造过程抽象

发表于 2022-07-15 更新于 2023-01-28 分类于 SICP

SICP 第一章

概要

线性递归、树形递归与迭代

过程抽象

（略）

线性递归与迭代

递归：一个过程的定义基于其自身

考虑计算阶乘$$\begin{split}n!=n·(n-1)·(n-1)···3×2×1\end{split}$$的实现：

第一种是，考虑到$$n!=n·[(n-1)·(n-2)···3×2×1] = n·(n-1)!$$故实现如下：

(define (factorial n)
    (if (= n 1) 
        1 
        (* n (factorial (- n 1)))))

上述代码运行(factorial 6)时计算过程如下图：
线性递归

这一计算过程构造了一个由推迟进行的操作形成的链条，需要保存的内存大小随n的值线性增长，故此计算过程称为一个线性递归过程，其代换模型先逐步展开后收缩。

第二种是，先乘起 1 和 2，再将结果一直乘下去。此时需要再内存中保存一个计数器counter以确保只乘到n，还需要保存临时的乘积product。两个变量按规律变化：

1 2	product = product * counter counter = counter + 1

故将其改写为：

(define (factorial n) (fact-iter 1 1 n))

(define (fact-iter product counter max-count) 
    (if (> counter max-count)
        product
        (fact-iter (* counter product) 
            (+ counter 1) 
            max-count)))

上述代码运行(factorial 6)时计算过程如下图：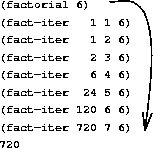
线性迭代

与先前的分析相对应，计算过程里并没有任何增长或者收缩。对于任何一个n，在计算过程中的每一步，在我们需要保存轨迹里，所有的东西就是变量product，counter和max-count的当前值。这是一个迭代计算过程。一般来说，迭代计算过程就是那种其状态可以用固定数目的状态变量描述的计算过程，状态变量遵守一套描述了计算过程在从一个状态到下一状态转换时这些变量的更新方式的固定规则和一个（可能有的）结束检测。在计算n!时，所需的计算步骤随着n线性增长，这种过程称为线性迭代过程。

树形递归

下面实现斐波那契数列$Fib(n)$：

$
Fib(n) =\begin{cases}
0, & n=0 \\
1, & n=1 \\
\small{Fib(n-1)} +\\
\quad \small{Fib(n-2),} & \text{其他}
\end{cases}
$

得：

(define (fib n)
    (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1 ))
                (fib (- n 2))))))

解释过程中，为了计算(fib 5)计算机需要先计算出(fib 4)和(fib 3)；为了计算(fib 4)计算机需要先计算出(fib 3)和(fib 2)。这一展开过程看起来像一棵树，每次计算都需要调用两次自身。

树形递归

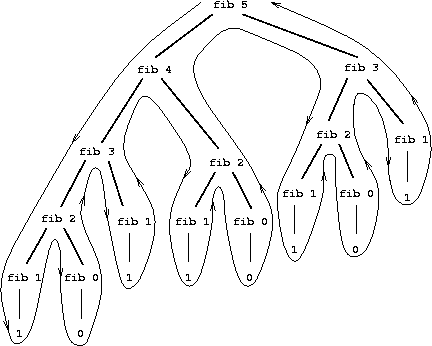
实际上，上述实现方式在计算过程中做了很多冗余计算，其计算量随n的增长而指数增长。在计算Fib(3)中先计算Fib(2)和Fib(1)，在计算Fib(2)中先计算Fib(1)和Fib(0)，不止一次地计算了3遍Fib(0)、2遍Fib(1)。

我们也可以使用迭代实现斐波那契数列：

a = Fib(1) = 1
b = Fib(0) = 0

a = a + b      // a为`Fib(n+1)`
b = a          // b为`Fib(n)`

(define (fib n) (fib-iter 1 0 n))

(define (fib-iter a b count)
    (if (= count 0)
        b
        (fib-iter (+ a b) a (- count 1))))

高阶函数抽象

过程就是一类描述一些对于数的复合操作的抽象，但又并不依赖于特定的数。如在定义:

1	(define (cube x) (* x x x))

时，我们讨论的并不是某个特定数值的立方，而是对任意的数得到其立方的方法。当然，我们也可以不去定义cube而总是写出下面这样的表达式：

1
2
3

(* 3 3 3)
(* x x x)
(* y y y)

但是，这迫使我们永远在语言恰好提供了的那些特定基本操作（例如这里的乘法）的层面上工作，而不能基于更高级的操作。人们对功能强大的程序设计语言有一个必然要求，就是能为公共的模式命名，建立抽象，而后直接在抽象的层次上工作。过程提供了这种能力，这也是为什么除最简单的程序语言外，其他语言都包含定义过程的机制的原因。

lambda 表达式

在进行高阶函数抽象时，我们必须先定义出一些简单函数以便用它们作为高阶函数的参数，这种做法看起来很不舒服。如果有一种方法去直接刻画那个函数，事情就会方便多了。我们可以引入一种 lambda 特殊形式完成这类描述，这种特殊形式能够创建出所需要的过程。利用 lambda，我们就能按照如下方式写出所需的东西：

1
2
3

; 用法：(lambda (<formal-parameters>) <body>)
(lambda (x) (+ x 4))
; 上式与`(define plus4 (lambda (x) (+ x 4)))`等价

我们可以这样理解 Lambda 表达式：

1 2	(lambda (x) (+ x 4)) the procedure of an argument x that adds x and 4

let 局部变量

在计算
$$f(x, y)=x(1+xy)^2 +y(1-y)+(1+xy)(1-y)$$
时，可以这样实现：
$$\begin{split}a=&1+xy \\
b=&1-y \\
f(x,y)=&xa^2+yb+ab\end{split}$$

同时在写计算$f$的过程时，我们可能希望还有几个局部变量中间值，如a和b。做到这些的一种方式就是利用辅助过程去约束局部变量:

(define (f x y)
  (define (f-helper a b)
    (+ (* x (square a))
       (* y b)
       (* a b)))
  (f-helper (+ 1 (* x y)) 
            (- 1 y)))

当然，我们也可以用一个lambda表达式以描述约束局部变量的匿名过程，即改写为：

(define (f x y)
  ((lambda (a b)
     (+ (* x (square a))
        (* y b)
        (* a b)))
   (+ 1 (* x y))
   (- 1 y)))

这一结构非常有用，因此sheme语言里有一个专门的特殊形式称为let，使这种编程方式更为方便。利用let，过程$f$可以写为:

(define (f x y)
  (let ((a (+ 1 (* x y)))
        (b (- 1 y)))
    (+ (* x (square a))
       (* y b)
       (* a b))))

(let ((<var-1> <exp-1>)
      (<var-2> <exp-2>)
      ...
      (<var-n> <exp-n>))
   <body>)

let表达式的第一部分是个名字-表达式对偶的表，当let被求值时，这里的每个名字将被关联于对应表达式的值。在将这些名字约束为局部变量的情况下求值let的体。这一做法正好使let表达式被解释为替代如下表达式的另一种语法形式：

((lambda (<var-1> ...<var-n>)
    <body>)
 <exp-1>
 ...
 <exp-n>)