DL/ML中的Uncertainty
什么是Uncertainty?简单的说,Uncertainty 就是让你的神经网络具有说“我不知道”的能力。
Uncertainty 相关的工作通过对不确定性进行评估让模型具有说“我不知道”的能力。
Uncertainty的分类
Uncertainty通常分为以下两种类型:
- Aleatoric Uncertainty(随机不确定性)指数据的不确定性。由于训练数据的有限性或采样不充分,导致模型对数据分布的理解不足,从而无法准确预测结果的不确定性。可以通过增加数据量、改变模型结构、修改模型参数等方式来降低。认知不确定性测量的是我们的input data是否存在于已经见过的数据的分布之中。降低的方法有:
- 数据增强:通过对训练数据进行旋转、翻转、缩放等操作,可以增加训练数据的数量和多样性。
- 数据平衡:通过对训练数据进行平衡处理,可以避免模型对某些类别的过拟合。
- 迁移学习:通过利用已有的大规模数据集进行迁移学习。
- Epistemic Uncertainty(认知不确定性)指模型的不确定性。对于同样的数据,我们可能训练出都可以解决问题但权重不同的神经网络,这些模型对于数据可以有不同的认知。训练过程中的错误、模型结构缺陷而导致的知识不足均可造成。降低的方法有:
- Monte Carlo Dropout:在训练期间随机去除一部分神经元,可以降低模型的过拟合。
- 贝叶斯神经网络:在贝叶斯神经网络中,模型的参数被建模为概率分布,可以通过后验分布来表示模型的不确定性。
- 参数剪枝:通过删除不必要的参数,可以降低模型的参数数量。
Uncertainty的评估
Calibration
Calibration Error = |Confidence - Accuracy|
Confidence: predicted probability of correctness
Accuracy: observed frequency of correctness
- 对于分类问题,完美校准意味着置信度为0.7的模型预测100次,那么刚好其中70个的预测是正确的。
- 对于回归问题,校准对应于置信区间内的覆盖率。
Expected Calibration Error(ECE)
$ECE = \sum_{b=1}^B \frac{n_b}{N} |\text{acc}(b) - \text{conf}(b)|$
Note: ECE不代表acc。比如:
True label 0 0 0 0 0 0 0 1 1 1 Accurate? Calibrated? Model prediction 0.3 0.3 0.3 0.3 0.3 0.3 0.3 0.3 0.3 0.3 No Yes
其他指标或方法
- 在out-of-distribution (OOD) inputs上评估模型
- Uncertainty-Error overlap,通常,分割任务不需要完美的校准,但是对于模型来说,确定哪里出错了并确定哪里正确就足够了。U-E其实表达的是分割错误区域和低置信度区域(阈值控制)之间的重合度。
- General Measures
- Accuracy/Dice ↑
- Prediction Variance ↓
- Predictive Entropy ↓
- Predictive variance ↓
- Mutual information ↓
- Negative Log-Likelihood(NLL)↓
- Brier Score ↓
- Expected Calibration Error(ECE)↓
- Structure-wise Measures
- Volume Variation ↓
- Dice Agreement ↑
- Intersection over union ↑
- Mean Uncertainty ↓
- Generalized Energy Distance ↓
稳健方法
Probabilistic Machine Learning
- 普通模型:$\theta^* = \arg \max p(\theta|x, y)$
- 贝叶斯概率视角下的模型:给定输入$x$的输出$y$和参数 $\theta^*$ 的联合分布。
$$
p(y, \theta|x)
$$ - 训练:
$$
p(\theta|x, y) = \frac{p(y, \theta|x)}{p(y | x)} = \frac{p(y, x)p(\theta)}{\int p(y, \theta|x)d \theta}
$$ - 推理:计算给定参数的可能性,每个参数配置都经过后验加权。
$$
p(y|x, \mathcal{D}) = \int p(y|x, \theta) p(\theta| \mathcal{D}) d \theta \approx \frac{1}{S} \sum_{s=1}^S p(y|x, \theta ^ {(s)})
$$
一般流程为:
- 获得基础模型 $ p(y, \theta|x)$
- 确定先验函数 $p(\theta)$
- 通过近似后验来捕获模型的不确定性 $ p(\theta| \mathcal{D})$
评估不确定性的方法有:
- 获得 $p(\theta|x, y)$
- 获得很多个 $\theta^*$
模型集成(bagging, boosting, stacking, 决策树)
uncertainty estimation via ensembling of networks
使用k个训练好的网络取平均,$p_c=\frac{1}{K}\sum^K_{k=1}p(y|x, \theta_k)$ 。每个独立的网络使用同样的模型算法,但使用不同的子集和不同的初始化参数训练。
还有深度模型集成方法,也是个simple baseline
Bayesian uncertainty estimation via test-time dropout
test-time dropout 可以认为是BNN的近似。T个随机dropout网络生成概率预测,将这些概率的归一化熵用作不确定性的度量,$p_c=\frac{1}{T}\sum^T_{t=1}p_{t,c}$。目前有两种dropout方法,一种是在每个卷积层后都加一个p=0.05的dropout(称为baseline+MC),另一种是在中心位置使用p=0.5的dropout(称为center+MC),两个方法同样使用T=20。
aleatoric uncertainty estimation via a second network output
MC dropout 衡量模型预测中存在的不确定性,偶然不确定性方法衡量观测中的固有噪声。这种方法学习一个函数 $f(x)$,输入训练数据 $x$ 得到两个输出 $[\hat x,\sigma^2]$,这两个输出是经过高斯噪声扰乱的logits的均质和方差。通过 aleatoric loss 来优化两个输出,同时将这两个输出作为uncertainty的度量。
Auxiliary network
辅助网络方法是用来预测样本级的分割表现的。有两个辅助网络:
- auxiliary feat,包括三个连续的1 $\times$ 1卷积网络与分割网络的最后一个特征层相连。
- auxiliary segm,是一个完全独立的U-net网络,网络的输入为原始图像和分割模型得到的分割mask。
应用
Domain Adaptation
利用Uncertainty修正Domain Adaptation中的伪标签
- IJCV | https://zhuanlan.zhihu.com/p/130220572
- 论文地址: https://arxiv.org/pdf/2003.03773.pdf
- 作者:Zhedong Zheng, Yi Yang
- 代码: https://github.com/layumi/Seg_Uncertainty
- 本文研究的是领域迁移问题中错误的伪标签(Pseudo Label)的问题,探讨了如何自动设定阈值来修正这种伪标签学习。
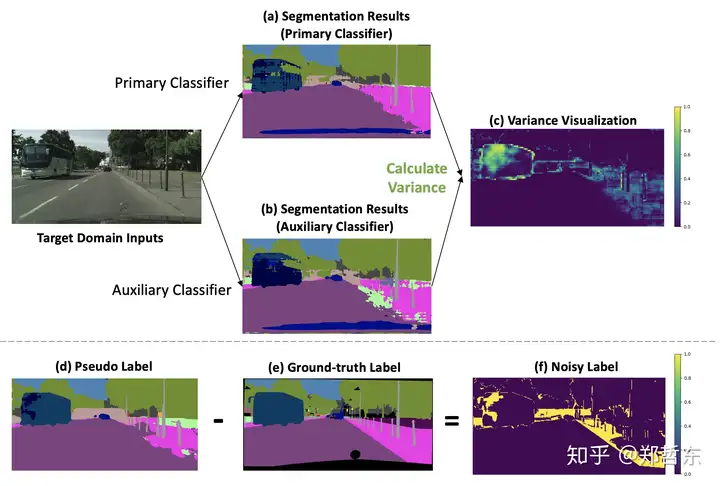
- 之前的伪标签往往通过人为卡阈值(Threshold) 的方式来学高置信度的伪标签(Pseudo Label),而忽略低置信度的标签。 但是这个阈值(Threshold) 往往很难决定。我们认为这个阈值取决于 source 和 target 有多接近,我们提出用不确定性来作为阈值,等同于自动学一个阈值出来。伪标签错误的地方,往往是 两个分类器预测不同结果的地方(Prediction Variance)
![Prediction Variance]()
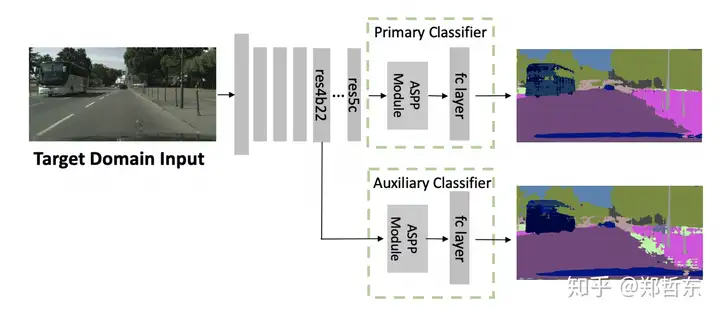
- 利用了分割模型中的辅助分类器得到两个分割结果
![辅助分类器]()
- 修改cross-entropy loss惩罚Prediction Variance
$$ L_{rect} = \mathbb{E}[exp{-D_{kl}}L_{ce}+ D_{kl}] $$
医学图像分割
医学图像分割领域,不确定性主要关注点在以下三个层次:
- 体素级别的uncertainty,这对于辅助医生的诊断至关重要
- 实例分割层面的不确定性(将体素不确定性汇总),能够降低错误率
- 样本层面的不确定性,这样能告诉我们当前得到的分割结果是否成功
几个简写
- TPU: uncertainty in the true positives
- TNU: uncertainty in the true negatives
- FPU: uncertainty in the false positives
- FNU: uncertainty in the false negatives
- BnF: benefit condition for false positive removal
当满足假阳性的不确定性FPU > 真阴性的不确定性TPU时,可以通过修正假阳性来提升Dice系数。